This section investigates the robustness of MaxDiff designs to prohibitions using Sawtooth Software's MaxDiff System and simulated (synthetic) respondent data.
The Case for Prohibitions
MaxDiff questionnaires present respondents with typically four to six items at a time and ask which item is "best" and which is "worst." In practice, enough sets are shown to the respondent such that each item occurs about two to five times. (In some applications, the "worst" question may be skipped altogether.) Sawtooth Software's MaxDiff component within Lighthouse Studio helps researchers design, field, and analyze MaxDiff studies very rapidly.
One advanced option in the software is the ability to specify that certain levels should never be paired within the same set. For example, in a fast-food restaurant study, we might wish to study the importance of the length of time to order and receive food. We might use three items in our MaxDiff design related to this:
Order and receive food within 3 minutes
Order and receive food within 5 minutes
Order and receive food within 10 minutes
When people go to fast-food restaurants, we presume they want to receive their food as quickly as possible. Therefore, it wouldn't make sense to show respondents a MaxDiff task in which any two of these items are paired. Respondents would always prefer the faster speed to slower, so this would be a wasted comparison.
Prohibitions and Design Efficiency
Those researchers familiar with conjoint analysis know that prohibiting certain level combinations from occurring in the conjoint questionnaire can often be very damaging to design efficiency (the ability of the questionnaire to estimate preference weights with precision). However, it turns out that prohibitions are generally not very harmful in MaxDiff questionnaires. We demonstrate that point below using simulated data sets with differing numbers of prohibitions.
Why are prohibitions more damaging in conjoint analysis than for MaxDiff? Prohibitions in conjoint analysis are "within-concept" and lead to correlations between attributes in the independent variable matrix. For MaxDiff, the prohibitions are "between-concept" and are less damaging to orthogonality. The reduction in design efficiency in MaxDiff studies from prohibitions is due in part from deviations from orthogonality. Other contributing factors are the imbalance that is sometimes introduced in the frequency of items and the reduction in the degree of interconnectivity among items. In optimal MaxDiff studies, each item is shown an equal number of times and is also compared an equal number of times with every other item. And, for any one respondent, we want to minimize the total number of steps that it takes to directly or indirectly compare all items. For example, if A is compared to B in question one and B is compared to C in question two, then A is "linked" to C through two steps.
"Gold Standard" Design with No Prohibitions
In a MaxDiff study involving 20 items, there are ½t(t-1) possible two-way combinations of items that can be prohibited. The ½(20)(19)=190 possible paired levels are represented by the white region of the table below:
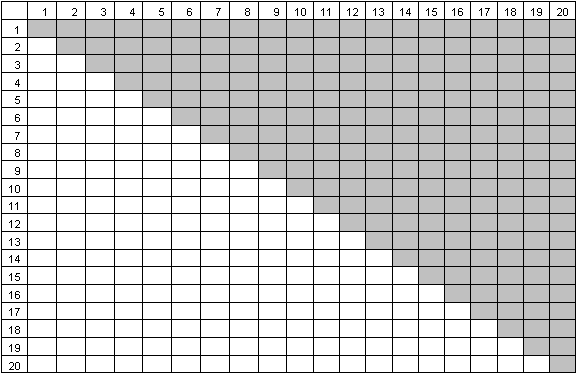
We begin by simulating data for a typical MaxDiff study that involves 20 items shown in sets of 4. Three-hundred computer-generated respondents each received a 20-set questionnaire and "answered" randomly ("bests" only). Each respondent received a unique version of the questionnaire, as generated by the MaxDiff designer.
To compute design efficiency, we estimate an aggregate logit model and observe the precision of the estimates (the standard errors). We also compute D-efficiency. The efficiency of one design relative to another is found by taking the ratios of the D-efficiencies for the two designs. The base case example (with no prohibitions) is our "gold standard" for comparison to designs with prohibitions.
Modest Prohibitions Case
First we implement a modest number of prohibitions. Let's consider that the last five items in the study are mutually exclusive, leading to the following prohibitions (prohibited levels marked with an "x"):
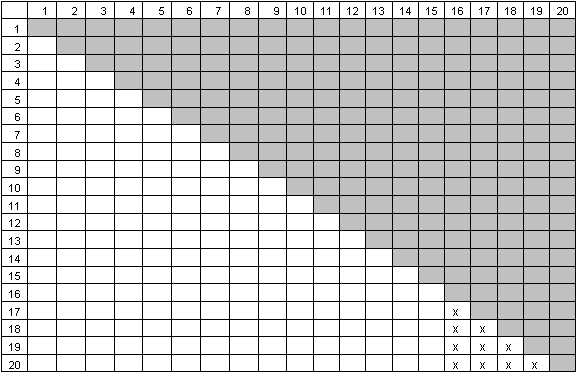
These ten prohibitions are grouped, with many occurring within the same row or column. This is potentially more damaging than if ten prohibitions were scattered randomly across the table. But, even these prohibitions have very little effect on design efficiency for MaxDiff. We generated a new series of questionnaires involving these prohibitions and again had 300 respondents answer randomly. The standard errors of the estimates were only slightly larger than in the non-prohibited case. This design is 99.99% as efficient as the "gold standard" design with no prohibitions. For all practical purposes, this design is as efficient as the "gold standard."
Extreme Case
Let's consider a much more extreme case. We'll retain the previous prohibitions, but add other prohibitions which at face value might seem to be quite damaging:
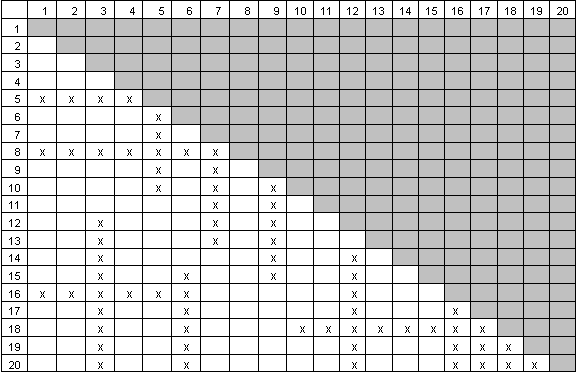
With these challenging (insane?) prohibitions, it becomes impossible for the MaxDiff designer to find a very balanced design. It returns an imbalanced solution wherein the most represented item (item #2) occurs over three times as often as the least represented (and most prohibited) item (item #18). The largest standard error occurs for item #18 with a standard error almost double that of the most precise estimates for items in the design with no prohibitions. While these results would be concerning, these prohibitions wouldn't ruin the MaxDiff project (especially if we had reasonable sample sizes). The overall relative design efficiency (considering all items) for this highly prohibited case is 92% as efficient as "gold standard" design.
"Conjoint-Style" Prohibitions
As a final example, MaxDiff may be used for "conjoint-style" brand x price experiments, such as was presented by Keith Chrzan in the 2003 Sawtooth Software Proceedings. Keith demonstrated the use of MaxDiff for pricing options on automobiles. Each option was tested at multiple prices (i.e. each item text included a description of the option plus its price). Thus, his project was a discrete choice study implemented as a MaxDiff exercise. An exercise like this is specified by developing a list of items (such as options for automobiles) where each option is displayed at different prices. Then, prohibitions are specified such that an item isn't shown twice (at different prices) within the same set.
Let's consider a study in which we have four options each at five prices. The prohibitions table looks like this:
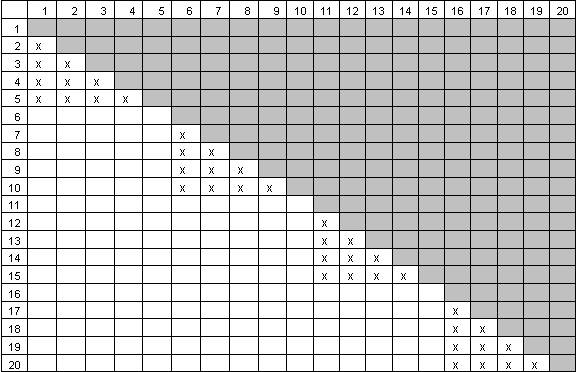
Repeating the simulation process with synthetic data, we find that this design is 99.5% as efficient as the "gold standard" plan with no prohibitions.
In this section, we've only considered statistical efficiency to assess the issue of prohibitions. We find that MaxDiff designs are remarkably robust to prohibitions. However, there may be additional considerations, such as context bias, that researchers may wish to consider when using prohibitions in MaxDiff questionnaires.